A1-2: Use of Books and Graph Drawing

Apparatus

Selection of Physics books; 4 or 5 figure log tables; 1 sheet of graph paper.

Procedure

  1. Use the books provided to answer the following:

    1. What is rectilinear motion?

    2. Name 3 ferromagnetic materials (is there a 4th?).

    3. What are the unit prefixes (letter and name) for:

      \(10^{12},\ 10^9,\ 10^6,\ 10^3,\ 10^2,\ 10^{-2}, 10^{-3},\ 10^{-6},\ 10^{-9},\ 10^{-12}\)

    4. What are the letters of the Greek alphabet? Give their names.

    5. What does ‘Non-Ohmic conductor’ mean? Give four examples.

    6. What is the velocity of sound in air at \(0 \text{°C}\)?

    7. \(0 \text{°C}\) equals how many K, exactly?

    8. What are the main types of experimental error?

    9. \(a = 5 \pm 0.005\text{m}\) and \(b = 3.5 \pm 0.01\text{m}\). What is the error in \(a+b\) in metres and in %? What is the % error in \(ab\)?

    10. Define the metre, the kilogram, the second, the newton, and the joule. Which are base units and why?

  2. Use 4- or 5-figure log tables to calculate the following:

      1. \(28.5 \times 137\)
      2. \(0.056 \times 55.62\)
      3. \(0.0335 \div 0.48\)
      4. \(73500 \div 0.6885\)
      5. \(5.322^4\)
      6. \(\sqrt[3]{6.03}\)
      7. \(\log (0.002)\)
      8. \(10^{1.3}\)
      1. \(\sin (26°\ 36')\)
      2. \(\cos^{-1}(0.391)\)
      3. \(\tan (53.552°)\)
      4. \(\tan (216°)\)
      5. \(\cos (126°)\)
      1. Convert to radians: \(\quad 90° \qquad 72° \qquad 200°\)
      2. Convert to degrees: \(\quad 1.12\text{rad} \qquad 3 \pi\text{rad} \qquad 3\pi/2\text{rad}\)
      1. \(\ln{(7.9)}\)
      2. \(e^{1.5}\)
      3. \(\ln (0.14)\)
      4. \(\ln (40)\)
      5. \(e^{15}\)
      6. \(e^{0.02}\)
      1. \(\sqrt{553}\)
      2. \(\sqrt{0.07}\)

  3. Graphs.

    1. In an Ohm’s Law experiment, where \(V = IR\), the following readings were obtained:

      A1-2.1

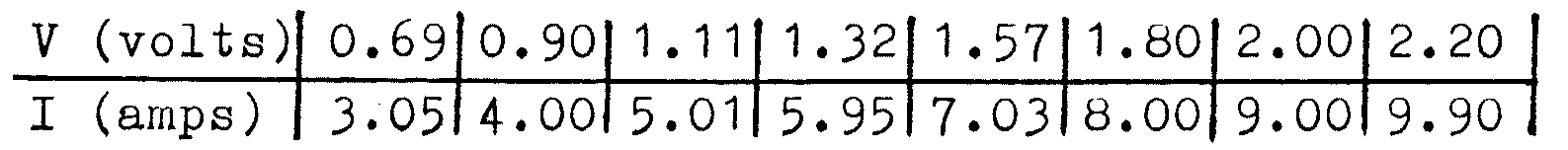
      Draw a graph of \(V\) against \(I\), and hence find \(R\).

    2. A cell of internal resistance \(r\) and emf \(E\) supplies current through a resistor \(R\). The equation which applies is:

      \[r=R \left(\frac{E-V}{V}\right)\]

      Readings of \(R\) and \(V\) are obtained, and \(1/R\) is plotted against \(1/V\). Explain how the gradient and \(y\)-intercept can be used to find \(E\) and \(r\).